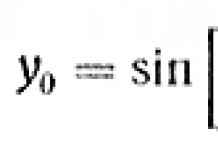Социальные и экономические объекты, как правило, характеризуются достаточно большим числом параметров, образующих многомерные векторы, и особое значение в экономических и социальных исследованиях приобретают задачи изучения взаимосвязей между компонентами этих векторов, причем эти взаимосвязи необходимо выявлять на основании ограниченного числа многомерных наблюдений.

Многомерным статистическим анализом называется раздел математической статистики, изучающий методы сбора и обработки многомерных статистических данных, их систематизации и обработки с целью выявления характера и структуры взаимосвязей между компонентами исследуемого многомерного признака, получения практических выводов.

Отметим, что способы сбора данных могут различаться. Так, если исследуется мировая экономика, то естественно взять в качестве объектов, на которых наблюдаются значения вектора X, страны, если же изучается национальная экономическая система, то естественно наблюдать значения вектора X на одной и той же (интересующей исследователя) стране в различные моменты времени.

Такие статистические методы, как множественный корреляционный и регрессионный анализ, традиционно изучаются в курсах теории вероятностей и математической статистики , рассмотрению прикладных аспектов регрессионного анализа посвящена дисциплина «Эконометрика» .

Другим методам исследования многомерных генеральных совокупностей на основании статистических данных посвящено данное пособие.

Методы снижения размерности многомерного пространства позволяют без существенной потери информации перейти от первоначальной системы большого числа наблюдаемых взаимосвязанных факторов к системе существенно меньшего числа скрытых (ненаблюдаемых) факторов, определяющих вариацию первоначальных признаков. В первой главе описываются методы компонентного и факторного анализа, с использованием которых можно выявлять объективно существующие, но непосредственно не наблюдаемые закономерности при помощи главных компонент или факторов.

Методы многомерной классификации предназначены для разделения совокупностей объектов (характеризующиеся большим числом признаков) на классы, в каждый из которых должны входить объекты, в определенном смысле однородные или близкие. Такую классификацию на основании статистических данных о значениях признаков на объектах можно провести методами кластерного и дискриминантного анализа, рассматриваемыми во второй главе (Многомерный статистический анализ с использованием “STATISTICA”).

Развитие вычислительной техники и программного обеспечения способствует широкому внедрению методов многомерного статистического анализа в практику. Пакеты прикладных программ с удобным пользовательским интерфейсом, такие как SPSS, Statistica, SAS и др., снимают трудности в применении указанных методов, заключающиеся в сложности математического аппарата, опирающегося на линейную алгебру, теорию вероятностей и математическую статистику, и громоздкости вычислений.

Однако применение программ без понимания математической сущности используемых алгоритмов способствует развитию у исследователя иллюзии простоты применения многомерных статистических методов, что может привести к неверным или необоснованным результатам. Значимые практические результаты могут быть получены только на основе профессиональных знаний в предметной области, подкрепленных владением математическими методами и пакетами прикладных программ, в которых эти методы реализованы.

Поэтому для каждого из рассматриваемых в данной книге методов приводятся основные теоретические сведения, в том числе алгоритмы; обсуждается реализация этих методов и алгоритмов в пакетах прикладных программ. Рассматриваемые методы иллюстрируются примерами их практического применения в экономике с использованием пакета SPSS.

Пособие написано на основе опыта чтения курса «Многомерные статистические методы» студентам Государственного университета управления. Для более подробного изучения методов прикладного многомерного статистического анализа рекомендуются книги .

Предполагается, что читатель хорошо знаком с курсами линейной алгебры (например, в объеме учебника и приложения к учебнику ), теории вероятностей и математической статистики (например, в объеме учебника ).

Введение

Глава 1. Множественный регрессионный анализ

Глава 2. Кластерный анализ

Глава 3. Факторный анализ

Глава 4. Дискриминантный анализ

Список используемой литературы

Введение

Исходная информация в социально-экономических исследованиях представляется чаще всего в виде набора объектов, каждый из которых характеризуется рядом признаков (показателей). Поскольку число таких объектов и признаков может достигать десятков и сотен, и визуальный анализ этих данных малоэффективен, то возникают задачи уменьшения, концентрации исходных данных, выявления структуры и взаимосвязи между ними на основе построения обобщенных характеристик множества признаков и множества объектов. Такие задачи могут решиться методами многомерного статистического анализа.

Многомерный статистический анализ - раздел статистики, посвященный математическим методам, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого и предназначенным для получения научных и практических выводов.

Основное внимание в многомерном статистическом анализе уделяется математическим методам построения оптимальных планов сбора, систематизации и обработки данных, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практических выводов.

Исходным массивом многомерных данных для проведения многомерного анализа обычно служат результаты измерения компонент многомерного признака для каждого из объектов исследуемой совокупности, т.е. последовательность многомерных наблюдений. Многомерный признак чаще всего интерпретируется как , а последовательность наблюдений как выборка из генеральной совокупности. В этом случае выбор метода обработки исходных статистических данных производится на основе тех или иных допущений относительно природы закона распределения изучаемого многомерного признака.

1. Многомерный статистический анализ многомерных распределений и их основных характеристик охватывает ситуации, когда обрабатываемые наблюдения имеют вероятностную природу, т.е. интерпретируются как выборка из соответствующей генеральной совокупности. К основным задачам этого подраздела относятся: оценивание статистическое исследуемых многомерных распределений и их основных параметров; исследование свойств используемых статистических оценок; исследование распределений вероятностей для ряда статистик, с помощью которых строятся статистические критерии проверки различных гипотез о вероятностной природе анализируемых многомерных данных.

2. Многомерный статистический анализ характера и структуры взаимосвязей компонент исследуемого многомерного признака объединяет понятия и результаты, присущие таким методам и моделям, как анализ, дисперсионный анализ, ковариационный анализ, факторный анализ и т.д. Методы, принадлежащие к этой группе, включают как алгоритмы, основанные на предположении о вероятностной природе данных, так и методы, не укладывающиеся в рамки какой-либо вероятностной модели (последние чаще относят к методам ).

3.Многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений объединяет понятия и результаты, свойственные таким моделям и методам, как дискриминантный анализ, кластерный анализ, многомерное шкалирование. Узловым для этих моделей является понятие расстояния, либо меры близости между анализируемыми элементами как точками некоторого пространства. При этом анализироваться могут как объекты (как точки, задаваемые в признаковом пространстве), так и признаки (как точки, задаваемые в объектном пространстве).

Прикладное значение многомерного статистического анализа состоит в основном в решении следующих трех задач:

· задача статистического исследования зависимостей между рассматриваемыми показателями;

· задача классификации элементов (объектов или признаков);

· задача снижения размерности рассматриваемого признакового пространства и отбора наиболее информативных признаков.

Множественный регрессионный анализ предназначен для построения модели, позволяющей по значениям независимых переменных получать оценки значений зависимой переменной.

Логистическая регрессия для решения задачи классификации. Это разновидность множественной регрессии, назначение которой состоит в анализе связи между несколькими независимыми переменными и зависимой переменной.

Факторный анализ занимается определением относительно небольшого числа скрытых (латентных) факторов, изменчивостью которых объясняется изменчивость всех наблюдаемых показателей. Факторный анализ направлен на снижение размерности рассматриваемой задачи.

Кластерный и дискриминантный анализ предназначены для разделения совокупностей объектов на классы, в каждый из которых должны входить объекты в определенном смысле однородные или близкие. При кластерном анализе заранее неизвестно, сколько получится групп объектов и какого они будут объема. Дискриминантный анализ разделяет объекты по уже существующим классам.

Глава 1. Множественный регрессионный анализ

Задание: Исследование рынка жилья в Орле (Советский и Северный районы).

В таблице приведены данные по цене квартир в Орле и по различным факторам, ее обусловливающим:

· общая площадь;

· площадь кухни;

· жилая площадь;

· тип дома;

· количество комнат. (Рис.1)

Рис. 1 Исходные данные

В графе «Район» использованы обозначения:

3 – Советский (элитный, относится к центральным районам);

4 – Северный.

В графе «Тип дома»:

1 – кирпичный;

0 – панельный.

Требуется:

1. Проанализировать связь всех факторов с показателем «Цена» и между собой. Отобрать факторы, наиболее подходящие для построения регрессионной модели;

2. Сконструировать фиктивную переменную, отображающую принадлежность квартиры к центральным и периферийным районам города;

3. Построить линейную модель регрессии для всех факторов, включив в нее фиктивную переменную. Пояснить экономический смысл параметров уравнения. Оценить качество модели, статистическую значимость уравнения и его параметров;

4. Распределить факторы (кроме фиктивной переменной) по степени влияния на показатель «Цена»;

5. Построить линейную модель регрессии для наиболее влиятельных факторов, оставив в уравнении фиктивную переменную. Оценить качество и статистическую значимость уравнения и его параметров;

6. Обосновать целесообразность или нецелесообразность включения в уравнение п. 3 и 5 фиктивной переменной;

7. Оценить интервальные оценки параметров уравнения с вероятностью 95%;

8. Определить, сколько будет стоить квартира общей площадью 74,5 м² в элитном (периферийном) районе.

Выполнение:

1. Проанализировав связь всех факторов с показателем «Цена» и между собой, были отобраны факторы, наиболее подходящие для построения регрессионной модели, используя метод включения «Forward»:

А) общая площадь;

В) количество комнат.

Включенные/исключенные переменные(a)

a Зависимая переменная: Цена

2. Переменная Х4 «Район» является фиктивной переменной, так как имеет 2 значения: 3-принадлежность к центральному району «Советский», 4- к периферийному району «Северный».

3. Построим линейную модель регрессии для всех факторов (включая фиктивную переменную Х4).

Полученная модель:

Оценка качества модели.

Стандартная ошибка = 126,477

Коэффициент Дарбина - Уотсона = 2,136

Проверка значимости уравнения регрессии

Значение критерия F-Фишера = 41,687

4. Построим линейную модель регрессию со всеми факторами (кроме фиктивной переменной Х4)

По степени влияния на показатель «Цена» распределили:

Самый значимый фактор – общая площадь (F= 40,806)

Второй по значимости фактор- количество комнат (F= 29,313)

5. Включенные/исключенные переменные

a Зависимая переменная: Цена

6. Построим линейную модель регрессии для наиболее влиятельных факторов с фиктивной переменной, в нашем случае она и является одним из влиятельных факторов.

Полученная модель:

У = 348,349 + 35,788 Х1 -217,075 Х4 +305,687 Х7

Оценка качества модели.

Коэффициент детерминации R2 = 0,807

Показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 89% вариации зависимой переменной учтено и обусловлено в модели влиянием включенных факторов.

Коэффициент множественной корреляции R = 0,898

Показывает тесноту связи между зависимой переменной У со всеми включенными в модель объясняющими факторами.

Стандартная ошибка = 126,477

Коэффициент Дарбина - Уотсона = 2,136

Проверка значимости уравнения регрессии

Значение критерия F-Фишера = 41,687

Уравнение регрессии следует признать адекватным, модель считается значимой.

Самый значимый фактор – количество комнат (F=41,687)

Второй по значимости фактор- общая площадь (F= 40,806)

Третий по значимости фактор- район (F= 32,288)

7. Фиктивная переменная Х4 является значимым фактором, поэтому целесообразно включить ее в уравнение.

Интервальные оценки параметров уравнения показывают результаты прогнозирования по модели регрессии.

С вероятностью 95% объем реализации в прогнозируемом месяце составит от 540,765 до 1080,147 млн. руб.

8. Определение стоимости квартиры в элитном районе

Для 1 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 3 + 305,687 * 1

Для 2 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 3 + 305,687 * 2

Для 3 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 3 + 305,687 * 3

в периферийном

Для 1 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 4 + 305,687 * 1

Для 2 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 4 + 305,687 * 2

Для 3 комн У = 348,349 + 35,788 * 74, 5 - 217,075 * 4 + 305,687 * 3

Глава 2. Кластерный анализ

Задание: Исследование структуры денежных расходов и сбережений населения.

В таблице представлена структура денежных расходов и сбережений населения по регионам Центрального федерального округа Российской федерации в 2003 г. Для следующих показателей:

· ПТиОУ – покупка товаров и оплата услуг;

· ОПиВ – обязательные платежи и взносы;

· ПН – приобретение недвижимости;

· ПФА – прирост финансовых активов;

· ДР – прирост (уменьшение) денег на руках у населения.

Рис. 8 Исходные данные

Требуется:

1) определить оптимальное количество кластеров для разбиения регионов на однородные группы по всем группировочным признакам одновременно;

2) провести классификацию областей иерархическим методом с алгоритмом межгрупповых связей и отобразить результаты в виде дендрограммы;

3) проанализировать основные приоритеты денежных расходов и сбережений в полученных кластерах;

Выполнение:

1) Определить оптимальное количество кластеров для разбиения регионов на однородные группы по всем группировочным признакам одновременно;

Для определения оптимального количества кластеров нужно воспользоваться Иерархическим кластерным анализом и обратиться к таблице «Шаги агломерации» к столбцу «Коэффициенты».

Эти коэффициенты подразумевают расстояние между двумя кластерами, определенное на основании выбранной дистанционной меры (Евклидово расстояние). На том этапе, когда мера расстояния между двумя кластерами увеличивается скачкообразно, процесс объединения в новые кластеры необходимо остановить.

В итоге, оптимальным считается число кластеров, равное разности количества наблюдений (17) и номера шага (14),после которого коэффициент увеличивается скачкообразно. Таким образом, оптимальное количество кластеров равно 3. (Рис.9)

статистический математический анализ кластерный

Рис. 9 Таблица «Шаги агломерации»

2) Провести классификацию областей иерархическим методом с алгоритмом межгрупповых связей и отобразить результаты в виде дендрограммы;

Теперь, используя оптимальное количество кластеров, проводим классификацию областей иерархическим методом. И в выходных данных обращаемся к таблице «Принадлежность к кластерам». (Рис.10)

Рис. 10 Таблица «Принадлежность к кластерам»

На Рис. 10 отчетливо видно, что в 3 кластер попали 2 области (Калужская, Московская) и г. Москва, во 2 кластер две (Брянская, Воронежская, Ивановская, Липецкая, Орловская, Рязанская, Смоленская, Тамбовская, Тверская), в 1 кластер – Белгородская, Владимирская, Костромская, Курская, Тульская, Ярославская.

Рис. 11 Дендрограмма

3) проанализировать основные приоритеты денежных расходов и сбережений, в полученных кластерах;

Для анализа полученных кластеров нам нужно провести «Сравнение средних». В выходном окне выводится следующая таблица (Рис. 12)

Рис. 12 Средние значения переменных

В таблице «Средних значений» мы можем проследить, каким структурам отдается наибольший приоритет в распределении денежных расходов и сбережений населения.

В первую очередь стоит отметить, что самый высокий приоритет во всех областях отдается покупке товаров и оплате услуг. Большее значение параметр принимает в 3 кластере.

2 место занимает прирост финансовых активов. Наибольшее значение в 1 кластере.

Наименьший коэффициент в 1 и 2 кластерах у «приобретение недвижимости», а в 3 кластере выявлено заметное уменьшение денег на руках у населения.

В целом особое значение для населения имеет покупка товаров и оплата услуг и незначительное покупка недвижимости.

4) сравнить полученную классификацию с результатами применения алгоритма внутригрупповых связей.

В анализе межгрупповых связей ситуация практически не изменилась, за исключением Тамбовской области, которая из 2 кластера попала в 1.(Рис.13)

Рис. 13 Анализ внутригрупповых связей

В таблице «Средних значений» никаких изменений не произошло.

Глава 3. Факторный анализ

Задание: Анализ деятельности предприятий легкой промышленности.

Имеются данные обследований 20 предприятий легкой промышленности (Рис. 14) по следующим характерным признакам:

· Х1 – уровень фондоотдачи;

· Х2 – трудоемкость единицы продукции;

· Х3 – удельный вес закупочных материалов в общих расходах;

· Х4 – коэффициент сменности оборудования;

· Х5 – премии и вознаграждения на одного работника;

· Х6 – удельный вес потерь от брака;

· Х7 – среднегодовая стоимость основных производственных фондов;

· Х8 – среднегодовой фонд заработной платы;

· Х9 – уровень реализуемости продукции;

· Х10 – индекс постоянного актива (отношение основных средств и прочих внеоборотных активов к собственным средствам);

· Х11 – оборачиваемость оборотных средств;

· Х12 – непроизводственные расходы.

Рис.14 Исходные данные

Требуется:

1. провести факторный анализ следующих переменных: 1,3,5-7, 9, 11,12, выявить и интерпретировать факторные признаки;

2. указать наиболее благополучные и перспективные предприятия.

Выполнение:

1. Провести факторный анализ следующих переменных: 1,3,5-7, 9, 11,12, выявить и интерпретировать факторные признаки.

Факторный анализ – это совокупность методов, которые на основе реально существующих связей объектов (признаков) позволяют выявить латентные (неявные) обобщающие характеристики организационной структуры.

В диалоговом окне факторного анализа выбираем наши переменные, указываем необходимые параметры.

Рис. 15 Полная объясненная дисперсия

По таблице «Полной объясненной дисперсии» видно, что выделены 3 фактора, объясняющие 74,8 % вариаций переменных – построенная модель достаточно хорошая.

Теперь интерпретируем факторные признаки по «Матрице повернутых компонент»: (Рис.16).

Рис. 16 Матрица повернутых компонент

Фактор 1 наиболее тесно связан с уровнем реализации продуктов и имеет обратную зависимость от непроизводственных расходов.

Фактор 2 наиболее тесно связан с удельным весом закупочных материалов в общих расходах и удельным весом потерь от брака и имеет обратную зависимость от премий и вознаграждений на одного работника.

Фактор 3 наиболее тесно связан с уровнем фондоотдачи и оборачиваемость оборотных средств и имеет обратную зависимость от среднегодовой стоимости основных производственных фондов.

2. Указать наиболее благополучные и перспективные предприятия.

Для того, чтобы выявить наиболее благополучные предприятия проведем сортировку данных по 3 факторным признакам по убыванию. (Рис.17)

Наиболее благополучными предприятиями следует считать: 13,4,5, так как в целом по 3 факторам их показатели занимают наиболее высокие и стабильные позиции.

Глава 4. Дискриминантный анализ

Оценка кредитоспособности юридических лиц в коммерческом банке

В качестве значимых показателей, характеризующих финансовое состояние организаций-заемщиков, банком выбраны шесть показателей (табл. 4.1.1):

QR (Х1) - коэффициент срочной ликвидности;

CR (Х2) - коэффициент текущей ликвидности;

EQ/TA (Х3) - коэффициент финансовой независимости;

TD/EQ (Х4) - суммарные обязательства к собственному капиталу;

ROS (Х5) - рентабельность продаж;

FAT (Х6) - оборачиваемость основных средств.

Таблица 4.1.1. Исходные данные

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS определить, к какой из четырех категорий относятся три заемщика (юридических лица), желающие получить кредит в коммерческом банке:

§ Группа 1 - с отличными финансовыми показателями;

§ Группа 2 - с хорошими финансовыми показателями;

§ Группа 3 - с плохими финансовыми показателями;

§ Группа 4 - с очень плохими финансовыми показателями.

По результатам расчета построить дискриминантные функции; оценить их значимость по коэффициенту Уилкса (λ). Построить карту восприятия и диаграммы взаимного расположения наблюдений в пространстве трех функций. Выполнить интерпретацию результатов проведенного анализа.

Ход выполнения:

Для того чтобы определить, к какой из четырех категорий относятся три заемщика, желающие получить кредит в коммерческом банке, строим дискриминантный анализ, который позволяет определить, к какой из ранее выявленных совокупностей (обучающих выборок) следует отнести новых клиентов.

В качестве зависимой переменной выберем группу, к которой может относиться заемщик в зависимости от его финансовых показателей. Из данных задачи, каждой группе присваивается соответствующая оценка 1, 2, 3 и 4.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.1.1, используются для построения уравнения дискриминантных функций D1(X), D2(X) и D3(X):

3.) D3(X) =

	1
(Константа)

Рис. 4.1.1. Коэффициенты канонической дискриминантной функции

Рис. 4.1.2. Лямбда Уилкса

Однако, поскольку значимость по коэффициенту Уилкса (рис. 4.1.2) второй и третей функции более 0.001, их для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.1.3) свидетельствуют о том, что для 100 % наблюдений классификация проведена корректно, высокая точность достигнута во всех четырех группах (100 %).

Рис. 4.1.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого заемщика приведены в таблице «Поточечные статистики» (рис. 4.1.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых заемщиков банка к обучающему подмножеству М1 – первый, второй и третий заемщик (порядковый номера 41, 42, 43) отнесены к подмножеству М1 с соответствующими вероятностями 100 %.

Номер наблюдения	Фактическая группа	Наивероятнейшая группа
		Предсказанная группа
	несгруппированные
	несгруппированные
	несгруппированные

Рис. 4.1.4. Поточечная статистика

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.1.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.1.6).

	1

Рис. 4.1.5. Функции в центроидах групп

Рис. 4.1.6. Карта восприятия для двух дискриминантных функций D1(X) и D2(X) (* - центроид группы)

Поле «Территориальной карты» разделено дискриминантными функциями на четыре области: в левой части находятся преимущественно наблюдения четвертой группы заемщиков с очень плохими финансовыми показателями, в правой части - первой группы с отличными финансовыми показателями, в средней и нижней части - третьей и второй группы заемщиков с плохими и хорошими финансовыми показателями соответственно.

Рис. 4.1.7. Диаграмма рассеяния для всех групп

На рис. 4.1.7 приведен объединенный график распределения всех групп заемщиков вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп заемщиков банка по финансовыми показателями. В правой части графика расположены заемщики с высокими показателями, в левой - с низкой, а в средней части - со средними финансовыми показателями. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

Оценка кредитоспособности физических лиц в коммерческом банке

Кредитный отдел коммерческого банка провел выборочное обследование 30 своих клиентов (физических лиц). На основе предварительного анализа данных, заемщики оценивались по шести показателям (табл. 4.2.1):

Х1 - заемщик брал кредит в коммерческих банках ранее;

Х2 - среднемесячный доход семьи заемщика, тыс. руб.;

Х3 - срок (период) погашения кредита, лет;

Х4 - размер выданного кредита, тыс. руб.;

Х5 - состав семьи заемщика, чел.;

Х6 - возраст заемщика, лет.

При этом по вероятности возврата кредита выявлены три группы заемщиков:

§ Группа 1 - с низкой вероятностью погашения кредита;

§ Группа 2 - со средней вероятностью погашения кредита;

§ Группа 3 - с высокой вероятностью погашения кредита.

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS необходимо классифицировать трех клиентов банка (по вероятности погашения кредита), т.е. оценить принадлежность каждого из них к одной из трех групп. По результатам расчета построить значимые дискриминантных функции, их значимость оценить по коэффициенту Уилкса (λ). В пространстве двух дискриминантных функций для каждой группы построить диаграммы взаимного расположения наблюдений и объединенную диаграмму. Оценить место расположения каждого заемщика на этих диаграммах. Выполнить интерпретацию результатов проведенного анализа.

Таблица 4.2.1. Исходные данные

Ход выполнения:

Для построения дискриминантного анализа в качестве зависимой переменной выберем вероятность своевременного погашения кредита клиентом. Учитывая, что она может быть низкой, средней и высокой, каждой категории присвоим соответствующую оценку 1,2 и 3.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.2.1, используются для построения уравнения дискриминантных функций D1(X), D2(X):

2.) D2(X) =

Рис. 4.2.1. Коэффициенты канонической дискриминантной функции

Рис. 4.2.2. Лямбда Уилкса

По коэффициенту Уилкса (рис. 4.2.2) для второй функции значимость более 0.001, следовательно, ее для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.2.3) свидетельствуют о том, что для 93,3 % наблюдений классификация проведена корректно, высокая точность достигнута в первой и второй группах (100% и 91,7%), менее точные результаты получены в третьей группе (88, 9%).

Рис. 4.2.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого клиента приведены в таблице «Поточечные статистики» (рис. 4.2.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых клиентов банка к обучающему подмножеству М3 – первый, второй и третий клиент (порядковый номера 31, 32, 33) отнесены к подмножеству М3 с соответствующими вероятностями 99%, 99% и 100%.

Номер наблюдения	Фактическая группа	Наивероятнейшая группа
		Предсказанная группа
	несгруппированные
	несгруппированные
	несгруппированные

Рис. 4.2.4. Поточечная статистика

Вероятность погашения кредита

Рис. 4.2.5. Функции в центроидах групп

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.2.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.2.6).

Поле «Территориальной карты» разделено дискриминантными функциями на три области: в левой части находятся преимущественно наблюдения первой группы клиентов с очень низкой вероятностью погашения кредита, в правой части - третьей группы с высокой вероятностью, в средней - второй группы клиентов со средней вероятностью возврата кредита соответственно.

На рис. 4.2.7 (а – в) отражено расположение клиентов каждой из трех групп на плоскости двух дискриминантных функций D1(X) и D2(X). По этим графикам можно проводить детальный анализ вероятности погашения кредита внутри каждой группы, судить о характере распределения клиентов и оценивать степень их удаленности от соответствующего центроида.

Рис. 4.2.6. Карта восприятия для трех дискриминантных функций D1(X) и D2(X) (* - центроид группы)

Так же на рис. 4.2.7 (г) в той же системе координат приведен объединенный график распределения всех групп клиентов вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп клиентов банка с разными вероятностями погашения кредита. В левой части графика расположены заемщики с высокой вероятностью погашения кредита, в правой - с низкой, а в средней части - со средней вероятностью. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

Рис. 4.2.7. Расположение наблюдений на плоскости двух дискриминантных функций для групп с низкой (а), средней (б), высокой (с) вероятностью погашения кредита и для всех групп (г)

Список литературы

1. «Многомерный статистический анализ в экономических задачах. Компьютерное моделирование в SPSS», , 2009 г.

2. Орлов А.И. «Прикладная статистика» М.: Издательство «Экзамен», 2004

3. Фишер Р.А. «Статистические методы для исследователей», 1954 г.

4. Калинина В.Н., Соловьев В.И. «Введение в многомерный статистический анализ» Учебное пособие ГУУ,2003;

5. Ахим Бююль, Петер Цёфель, «SPSS: искусство обработки информации» Изд-во DiaSoft, 2005г.;

6. http://ru.wikipedia.org/wiki

МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ

Раздел математич. статистики, посвященный математич. методам построения оптимальных планов сбора, систематизации и обработки многомерных статистич. данных, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака и предназначенным для получения научных и практич. выводов. Под многомерным признаком понимается р-мерный показателей (признаков, переменных) среди к-рых могут быть: количественные, т. е. скалярно измеряющие в определенной шкале проявления изучаемого свойства объекта, п о-рядковые (или ординальные), т. е. позволяющие упорядочивать анализируемые объекты по степени проявления в них изучаемого свойства; и классификационные (или номинальные), т. е. позволяющие разбивать исследуемую совокупность объектов на не поддающиеся упорядочиванию однородные (по анализируемому свойству) классы. Результаты измерения этих показателей

на каждом из побъектов исследуемой совокупности образуют многомерных наблюдений, или исходный массив многомерных данных для проведения М. с. а. Значительная часть М. с. а. обслуживает ситуации, в к-рых исследуемый многомерный признак интерпретируется как многомерная и соответственно последовательность многомерных наблюдений (1) - как из генеральной совокупности. В этом случае выбор методов обработки исходных статистич. данных и анализ их свойств производится на основе тех или иных допущений относительно природы многомерного (совместного) закона распределения вероятностей

Многомерный статистический анализ многомерных распределений и их основных характеристик охватывает лишь ситуации, в к-рых обрабатываемые наблюдения (1) имеют вероятностную природу, т. е. интерпретируются как выборка из соответствующей генеральной совокупности. К основным задачам этого подраздела относятся: статистич. оценивание исследуемых многомерных распределений, их основных числовых характеристик и параметров; исследование свойств используемых статистич. оценок; исследование распределений вероятностей для ряда статистик, с помощью к-рых строятся статистич. критерии проверки различных гипотез о вероятностной природе анализируемых многомерных данных. Основные результаты относятся к частному случаю, когда исследуемый признак подчинен многомерному нормальному закону распределения функция плотности к-рого задается соотношением

где - вектор математич. ожиданий компонент случайной величины , т. е.- ковариационная матрица случайного вектора , т. е.- ковариации компонент вектора (рассматривается невырожденный случай, когда ; в противном случае, т. е. при ранге , все результаты остаются справедливыми, но применительно к подпространству меньшей размерности , в к-рой оказывается сосредоточенным исследуемого случайного вектора ).

Так, если (1) - последовательность независимых наблюдений, образующих случайную выборку из то оценками максимального правдоподобия для параметров и , участвующих в (2), являются соответственно статистики (см. , )

причем случайный вектор подчиняется р-мерному нормальному закону и не зависит от , а совместное распределение элементов матрицы описывается т. н. распределением Уиша р-т а (см. ), к-рого

В рамках этой же схемы исследованы распределения и моменты таких выборочных характеристик многомерной случайной величины, как коэффициенты парной, частной и множественной корреляции, обобщенная (т. е. ), обобщенная -статистике Хотеллинга (см. ). В частности (см. ), если определить в качестве выборочной ковариационной матрицы подправленную "на несмещенность" оценку , а именно:

то случайной величины стремится к при , а случайные величины

подчиняются F-распределениям с числами степеней свободы соответственно (р, п-р) и (р, п 1 +п 2 -р-1). В соотношении (7) п 1 и n 2 - объемы двух независимых выборок вида (1), извлеченных из одной и той же генеральной совокупности - оценки вида (3) и (4)-(5), построенные по i-й выборке, а

Общая выборочная ковариационная , построенная по оценкам и

Многомерный статистический анализ характера и структуры взаимосвязей компонент исследуемого многомерного признака объединяет в себе понятия и результаты, обслуживающие такие методы и модели М. с. а., как множественная , многомерный дисперсионный анализ и ковариационный анализ, факторный анализ и метод главных компонент, анализ канонич. корреляций. Результаты, составляющие содержание этого подраздела, могут быть условно разделены на два основных типа.

1) Построение наилучших (в определенном смысле) статистич. оценок для параметров упомянутых моделей и анализ их свойств (точности, а в вероятностной постановке - законов их распределения, доверительных: областей и т. д.). Так, пусть исследуемый многомерный признак интерпретируется как векторная случайная , подчиненная р-мерному нормальному распределению , и расчленен на два подвектора--столбца и размерности qи р-qсоответственно. Это определяет и соответствующее расчленение вектора математич. ожиданий , теоретической и выборочной ковариационных матриц , а именно:

Тогда (см. , ) подвектора (при условии, что второй подвектор принял фиксированное значение ) будет также нормальным ). При этом оценками максимального правдоподобия. для матриц регрессионных коэффициентов и ковариацин этой классической многомерной модели множественной регрессии

будут взаимно независимые статистики соответственно

здесь распределение оценки подчинено нормальному закону , а оценки п - закону Уишарта с параметрами и (элементы ковариационной матрицы выражаются в терминах элементов матрицы ).

Основные результаты по построению оценок параметров и исследованию их свойств в моделях факторного" анализа, главных компонент и канонич. корреляций относятся к анализу вероятностно-статистич. свойств собственных (характеристических) значений и векторов различных выборочных ковариационных матриц.

В схемах, не укладывающихся в рамки классич. нормальной модели и тем более в рамки какой-либо вероятностной модели, основные результаты относятся к построению алгоритмов (и исследованию их свойств) вычисления оценок параметров, наилучших с точки зрения нек-poro экзогенно заданного функционала качества (пли адекватности) модели.

2) Построение статистич. критериев для проверки различных гипотез о структуре исследуемых взаимосвязей. В рамках многомерной нормальной модели (последовательности наблюдений вида (1) интерпретируются как случайные выборки из соответствующих многомерных нормальных генеральных совокупностей) построены, напр., статистич. критерии для проверки следующих гипотез.

I. Гипотезы о равенстве вектора математич. ожиданий исследуемых показателей заданному конкретному вектору ; проверяется с помощью -статистики Хотеллинга с подстановкой в формулу (6)

II. Гипотезы о равенстве векторов математич. ожиданий в двух генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных двумя выборками; проверяется с помощью статистики (см. ).

III. Гипотезы о равенстве векторов математич. ожиданий в нескольких генеральных совокупностях (с одинаковыми, но неизвестными ковариационными матрицами), представленных своими выборками; проверяется с помощью статистики

в к-рой есть i-е р-мерное наблюдение в выборке объема , представляющей j-ю генеральную совокупность, а и - оценки вида (3), построенные соответственно отдельно по каждой из выборок и по объединенной выборке объема

IV. Гипотезы об эквивалентности нескольких нормальных генеральных совокупностей, представленных своими выборками проверяется с помощью статистики

в к-рой - оценка вида (4), построенная отдельно по наблюдениям j- йвыборки, j=1, 2, ... , k.

V. Гипотезы о взаимной независимости подвекторов-столбцов размерностей соответственно на к-рые расчленен исходный р-мерный вектор исследуемых показателей проверяется с помощью статистики

в к-рой и - выборочные ковариационные матрицы вида (4) для всего вектора и для его подвектора x (i) соответственно.

Многомерный статистический анализ геометрической структуры исследуемой совокупности многомерных наблюдений объединяет в себе понятия и результаты таких моделей и схем, как дискриминантный анализ, смеси вероятностных распределений, кластер-анализ и таксономия, многомерное шкалирование. Узловым во всех этих схемах является понятие расстояния (меры близости, меры сходства) между анализируемыми элементами. При этом анализируемыми могут быть как реальные объекты, на каждом из к-рых фиксируются значения показателей ,- тогда геометрич. образом i-го обследованного объекта будет точка в соответствующем р-мерном пространстве, так и сами показатели - тогда геометрич. образом l-го показателя будет точка в соответствующем n-мерном пространстве.

Методы и результаты дискриминантного анализа (см. , , ) направлены на следующей задачи. Известно о существовании определенного числа генеральных совокупностей и у исследователя имеется по одной выборке из каждой совокупности ("обучающие выборки"). Требуется построить основанное на имеющихся обучающих выборках наилучшее в определенном смысле классифицирующее правило, позволяющее приписать нек-рый новый элемент (наблюдение ) к своей генеральной совокупности в ситуации, когда исследователю заранее не известно, к какой из совокупностей этот элемент принадлежит. Обычно под классифицирующим правилом понимается последовательность действий: по вычислению скалярной функции от исследуемых показателей, по значениям к-рой принимается решение об отнесении элемента к одному из классов (построение дискриминантной функции); по упорядочению самих показателей по степени их информативности с точки зрения правильного отнесения элементов к классам; по вычислению соответствующих вероятностей ошибочной классификации.

Задача анализа смесей распределений вероятностей (см. ) чаще всего (но не всегда) возникает также в связи с исследованием "геометрической структуры" рассматриваемой совокупности. При этом понятие r-го однородного класса формализуется с помощью генеральной совокупности, описываемой нек-рым (как правило, унимодальным) законом распределения так что распределение общей генеральной совокупности, из к-рой извлечена выборка (1), описывается смесью распределений вида где p r - априорная вероятность (удельный элементов) r-го класса в общей генеральной совокупности. Задача состоит в "хорошем" статистич. оценивании (по выборке ) неизвестных параметров а иногда и к. Это, в частности, позволяет свести задачу классификации элементов к схеме дискриминантного анализа, хотя в данном случае отсутствовали обучающие выборки.

Методы и результаты кластер-анализа (классификации, таксономии, распознавании образов "без учителя", см. , , ) направлены на решение следующей задачи. Геометрич. анализируемой совокупности элементов задана либо координатами соответствующих точек (т. е. матрицей ... , п), либо набором геометрич. характеристик их взаимного расположения, напр, матрицей попарных расстояний . Требуется разбить исследуемую совокупность элементов на сравнительно небольшое (заранее известное или нет) классов так, чтобы элементы одного класса находились на небольшом расстоянии друг от друга, в то время как разные классы были бы по возможности достаточно взаимоудалены один от другого и не разбивались бы на столь же удаленные друг от друга части.

Задача многомерного шкалирования (см. ) относится к ситуации, когда исследуемая совокупность элементов задана с помощью матрицы попарных расстояний и заключается в приписывании каждому из элементов заданного числа (р)координат таким образом, чтобы структура попарных взаимных расстояний между элементами, измеренных с помощью этих вспомогательных координат, в среднем наименее отличались бы от заданной. Следует заметить, что основные результаты и методы кластер-анализа и многомерного шкалирования развиваются обычно без каких-либо допущении о вероятностной природе исходных данных.

Прикладное назначение многомерного статистического анализа состоит в основном в обслуживании следующих трех проблем.

Проблема статистического исследования зависимостей между анализируемыми показателями. Предполагая, что исследуемый набор статистически регистрируемых показателей xразбит, исходя из содержательного смысла этих показателей и окончательных целей исследования, на q-мернын подвектор предсказываемых (зависимых) переменных и (р-q)-мерный подвектор предсказывающих (независимых) переменных, можно сказать, что проблема состоит в определении на основании выборки (1) такой q-мерной векторной функции из класса допустимых решений F, к-рая давала бы наилучшую, в определенном смысле, аппроксимацию поведения подвектора показателей . В зависимости от конкретного вида функционала качества аппроксимации и природы,анализируемых показателей приходят к тем или иным схемам множественной регрессии, дисперсионного, ковариационного или конфлюентного анализа.

Проблема классификации элементов (объектов или показателей) в общей (нестрогой) постановке заключается в том, чтобы всю анализируемую совокупность элементов, статистически представленную в виде матрицы или матрицы разбить на сравнительно небольшое число однородных, в определенном смысле, групп . В зависимости от природы априорной информации и конкретного вида функционала, задающего критерий качества классификации, приходят к тем или иным схемам дискриминантного анализа, кластер-анализа (таксономии, распознавания образов "без учителя"), расщепления смесей распределений.

Проблема снижения размерности исследуемого факторного пространства и отбора наиболее информативных показателей заключается в определении такого набора сравнительно небольшого числа показателен найденного в классе допустимых преобразований исходных показателей на к-ром достигается верхняя нек-рой экзогенно заданной меры информативности m-мерной системы признаков (см. ). Конкретизация функционала, задающего меру автоинформативности (т. е. нацеленное на максимальное сохранение информации, содержащейся в статистич. массиве (1) относительно самих исходных признаков), приводит, в частности, к различным схемам факторного анализа и главных компонент, к методам экстремальной группировки признаков. Функционалы, задающие меру внешней информативности, т. е. нацеленные на извлечение из (1) максимальной информации относительно нек-рых других, не содержащихся непосредственно в ж, показателен или явлений, приводят к различным методам отбора наиболее информативных показателей в схемах статистич. исследования зависимостей и дискриминантного анализа.

Основной математический инструментарий М. с. а. составляют специальные методы теории систем линейных уравнений и теории матриц (методы решения простой и обобщенной задачи о собственных значениях и векторах; простое обращение и псевдообращение матриц; процедуры диагонализации матриц и т. д.) и нек-рые оптимизационные алгоритмы (методы покоординатного спуска, сопряженных градиентов, ветвей и границ, различные версии случайного поиска и стохастич. аппроксимации и т. д.).

Лит. : Андерсон Т., Введение в многомерный статистический анализ, пер. с англ., М., 1963; Кендалл М. Дж.., Стьюарт А., Многомерный статистический анализ и временные ряды, пер. с англ., М., 1976; Большев Л. Н., "Bull. Int. Stat. Inst.", 1969, № 43, p. 425-41; Wishаrt .J., "Biometrika", 1928, v. 20A, p. 32-52: Hotelling H., "Ann. Math. Stat.", 1931, v. 2, p. 360-78; [в] Кruskal J. В., "Psychometrika", 1964, v. 29, p. 1-27; Айвазян С. А., Бежаева 3. И., . Староверов О. В., Классификация многомерных наблюдений, М., 1974.

С. А. Айвазян.

Математическая энциклопедия. - М.: Советская энциклопедия . И. М. Виноградов . 1977-1985 .

Справочник технического переводчика

Раздел статистики математической (см.), посвященный математич. методам, направленным на выявление характера и структуры взаимосвязей между компонентами исследуемого многомерного признака (см.) и предназначенным для получения научн. и практич.… …

В широком смысле раздел математической статистики (См. Математическая статистика), объединяющий методы изучения статистических данных, относящихся к объектам, которые характеризуются несколькими качественными или количественными… … Большая советская энциклопедия

АНАЛИЗ МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ - раздел математической статистики, предназначенный для анализа связей между тремя и более переменными. Можно условно выделить три основных класса задач А.М.С. Это исследование структуры связей между переменными и снижение размерности пространства … Социология: Энциклопедия

АНАЛИЗ КОВАРИАЦИОННЫЙ - – сово­купность методов математич. статистики, отно­сящихся к анализу моделей зависимости среднего значения нек рой случайной величины Y от набора неколичественных факторов F и одновременно от набора количественных факторов X. По отношению к Y… … Российская социологическая энциклопедия

Раздел математич. статистики, содержанием к рого является разработка и исследование статистич. методов решения следующей задачи различения (дискриминации): основываясь на результатах наблюдений, определить, какой из нескольких возможных… … Математическая энциклопедия, Орлова Ирина Владленовна, Концевая Наталья Валерьевна, Турундаевский Виктор Борисович. Книга посвящена многомерному статистическому анализу (МСА) и организации вычислений по МСА. Для реализации методов многомерной статистики используется программаобработки статистической…

По эконометрике

Многомерный статистический анализ

В многомерном статистическом анализе выборка состоит из элементов многомерного пространства. Отсюда и название этого раздела эконометрических методов. Из многих задач многомерного статистического анализа рассмотрим две - восстановления зависимости и классификации.

Оценивание линейной прогностической функции

Начнем с задачи точечного и доверительного оценивания линейной прогностической функции одной переменной.

Исходные данные – набор n пар чисел (t k , x k), k = 1,2,…,n, где t k – независимая переменная (например, время), а x k – зависимая (например, индекс инфляции, курс доллара США, объем месячного производства или размер дневной выручки торговой точки). Предполагается, что переменные связаны зависимостью

x k = a (t k - t ср)+ b + e k , k = 1,2,…,n,

где a и b – параметры, неизвестные статистику и подлежащие оцениванию, а e k – погрешности, искажающие зависимость. Среднее арифметическое моментов времени

t ср = (t 1 + t 2 +…+t n) / n

введено в модель для облегчения дальнейших выкладок.

Обычно оценивают параметры a и b линейной зависимости методом наименьших квадратов. Затем восстановленную зависимость используют для точечного и интервального прогнозирования.

Как известно, метод наименьших квадратов был разработан великим немецким математиком К. Гауссом в 1794 г. Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость x от t, следует рассмотреть функцию двух переменных

Оценки метода наименьших квадратов - это такие значения a* и b*, при которых функция f(a,b) достигает минимума по всем значениям аргументов.

Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b) по аргументам a и b, приравнять их 0, затем из полученных уравнений найти оценки: Имеем:

Преобразуем правые части полученных соотношений. Вынесем за знак суммы общие множители 2 и (-1). Затем рассмотрим слагаемые. Раскроем скобки в первом выражении, получим, что каждое слагаемое разбивается на три. Во втором выражении также каждое слагаемое есть сумма трех. Значит, каждая из сумм разбивается на три суммы. Имеем:

Приравняем частные производные 0. Тогда в полученных уравнениях можно сократить множитель (-2). Поскольку

(1)

уравнения приобретают вид

Следовательно, оценки метода наименьших квадратов имеют вид

(2)
В силу соотношения (1) оценку а* можно записать в более симметричном виде:

Эту оценку нетрудно преобразовать и к виду

Следовательно, восстановленная функция, с помощью которой можно прогнозировать и интерполировать, имеет вид

x*(t) = a*(t - t ср)+ b*.

Обратим внимание на то, что использование t ср в последней формуле ничуть не ограничивает ее общность. Сравним с моделью вида

x k = c t k + d + e k , k = 1,2,…,n.

Ясно, что

Аналогичным образом связаны оценки параметров:

Для получения оценок параметров и прогностической формулы нет необходимости обращаться к какой-либо вероятностной модели. Однако для того, чтобы изучать погрешности оценок параметров и восстановленной функции, т.е. строить доверительные интервалы для a*, b* и x*(t), подобная модель необходима.

Непараметрическая вероятностная модель. Пусть значения независимой переменной t детерминированы, а погрешности e k , k = 1,2,…,n, - независимые одинаково распределенные случайные величины с нулевым математическим ожиданием и дисперсией

неизвестной статистику.

В дальнейшем неоднократно будем использовать Центральную Предельную Теорему (ЦПТ) теории вероятностей для величин e k , k = 1,2,…,n (с весами), поэтому для выполнения ее условий необходимо предположить, например, что погрешности e k , k = 1,2,…,n, финитны или имеют конечный третий абсолютный момент. Однако заострять внимание на этих внутриматематических "условиях регулярности" нет необходимости.

Асимптотические распределения оценок параметров. Из формулы (2) следует, что

(5)

Согласно ЦПТ оценка b* имеет асимптотически нормальное распределение с математическим ожиданием b и дисперсией

оценка которой приводится ниже.

Из формул (2) и (5) вытекает, что

Последнее слагаемое во втором соотношении при суммировании по i обращается в 0, поэтому из формул (2-4) следует, что

(6)

Формула (6) показывает, что оценка

является асимптотически нормальной с математическим ожиданием и дисперсией

Отметим, что многомерная нормальность имеет быть, когда каждое слагаемое в формуле (6) мало сравнительно со всей суммой, т.е.

Из формул (5) и (6) и исходных предположений о погрешностях вытекает также несмещенность оценок параметров.

Несмещенность и асимптотическая нормальность оценок метода наименьших квадратов позволяют легко указывать для них асимптотические доверительные границы (аналогично границам в предыдущей главе) и проверять статистические гипотезы, например, о равенстве определенным значениям, прежде всего 0. Предоставляем читателю возможность выписать формулы для расчета доверительных границ и сформулировать правила проверки упомянутых гипотез.

Асимптотическое распределение прогностической функции. Из формул (5) и (6) следует, что

т.е. рассматриваемая оценка прогностической функции является несмещенной. Поэтому

При этом, поскольку погрешности независимы в совокупности и

, то

Таким образом,

Из предисловия автора
Глава 1. Введение
1.1. Многомерное нормальное распределение как модель
1.2. Общий обзор многомерных методов
Литература
Глава 2. Многомерное нормальное распределение
2.1. Введение
2.2. Понятия, связанные с многомерными распределениями
2.3. Многомерное нормальное распределение
2.4. Распределение линейной комбинации нормально распределенных величин; независимость величин; частные распределения
2.5. Условные распределения и множественный коэффициент корреляции
2.6. Характеристическая функция; моменты
Литература
Задачи
Глава 3. Оценка вектора среднего значения и ковариационной матрицы
3.1. Введение
3.2. Оценки наибольшего правдоподобия для вектора среднего значения и ковариационной матрицы
3.3. Распределение вектора выборочного среднего; заключение о среднем значении, когда ковариационная матрица известна
Литература
Задачи
Глава 4. Распределения и использование выборочных коэффициентов корреляции
4.1. Введение
4.2. Коэффициент корреляции двумерной выборки
4.3. Частные коэффициенты корреляции
4.4. Множественный коэффициент корреляции
Литература
Задачи
Глава 5. Обобщенная T2-статистика
5.1. Введение
5.2. Обобщенная T2-статистика и ее распределение
5.3. Применения T2-статистики
5.4. Распределение T2-статистики при наличии конкурирующих гипотез; функция мощности
5.5. Некоторые оптимальные свойства критерия Т2
5.6. Многомерная проблема Беренса - Фишера
Литература
Задачи
Глава 6. Классификация наблюдений
6.1. Проблема классификации
6.2. Принципы правильной классификации
6.3. Методы классификации наблюдений в случае двух генеральных совокупностей с известным распределением вероятностей
6.4. Классификация наблюдений в случае двух генеральных совокупностей, имеющих известные многомерные нормальные распределения
6.5. Классификация наблюдений в случае двух многомерных нормальных генеральных совокупностей, параметры которых оцениваются по выборке
6.6. Классификация наблюдений в случае нескольких генеральных совокупностей
6.7. Классификация наблюдений в случае нескольких многомерных нормальных совокупностей
6.8. Пример классификации в случае нескольких многомерных нормальных генеральных совокупностей
Литература
Задачи
Глава 7. Распределение выборочной ковариационной матрицы и выборочной обобщенной дисперсии
7.1. Введение
7.2. Распределение Уишарта
7.3. Некоторые свойства распределения Уишарта
7.4. Теорема Кохрена
7.5. Обобщенная дисперсия
7.6. Распределение множества коэффициентов корреляции в случае диагональной ковариационной матрицы совокупности
Литература
Задачи
Глава 8. Проверка общих линейных гипотез. Дисперсионный анализ
8.1. Введение
8.2. Оценки параметров многомерной линейной регрессии
8.3. Критерии отношения правдоподобия для проверки линейных гипотез о коэффициентах регрессии
8.4. Моменты отношения правдоподобия в случае, когда справедлива нулевая гипотеза
8.5. Некоторые распределения величин U
8.6. Асимптотическое разложение распределения отношения правдоподобия
8.7. Проверка гипотез о матрицах коэффициентов регрессии и доверительные области
8.8. Проверка гипотезы о равенстве средних значений нормальных распределений с общей ковариационной матрицей
8.9. Обобщенный дисперсионный анализ
8.10. Другие критерии для проверки линейной гипотезы
8.11. Каноническая форма
Литература
Задачи
Глава 9. Проверка гипотезы о независимости множеств случайных величин
9.1. Введение
9.2. Отношение правдоподобия как критерий для проверки гипотезы о независимости множеств случайных величин
9.3. Моменты отношения правдоподобия при условии, что справедлива нулевая гипотеза
9.4. Некоторые распределения отношения правдоподобия
9.5. Асимптотическое разложение распределения величины h (отношения правдоподобия)
9.6. Пример
9.7. Случай двух множеств случайных величин
Литература
Задачи
Глава 10. Проверка гипотез о равенстве ковариационных матриц и о равенстве одновременно векторов среднего значения и ковариационных матриц
10.1 Введение
10.2 Критерии проверки гипотез о равенстве нескольких ковариационных матриц
10.3. Критерии проверки гипотезы об эквивалентности нескольких нормальных совокупностей
10.4. Моменты отношения правдоподобия
10.5. Асимптотические разложения функций распределения величин V1 и V
10.6. Случай двух генеральных совокупностей
10.7. Проверка гипотезы о том, что ковариационная матрица пропорциональна заданной матрице. Критерий сферичности
10.8. Проверка гипотезы о том, что ковариационная матрица равна данной матрице
10.9. Проверка гипотезы о том, что вектор среднего значения и ковариационная матрица соответственно равны данному вектору и данной матрице
Литература
Задачи
Глава 11. Главные компоненты
11.1. Введение
11.2. Определение главных компонент совокупности
11.3. Оценки наибольшего правдоподобия для главных компонент и их дисперсий
11.4. Вычисление оценок наибольшего правдоподобия для главных компонент
11.5. Пример
Литература
Задачи
Глава 12. Канонические корреляции и канонические величины
12.1. Введение
12.2. Канонические корреляции и канонические величины генеральной совокупности
12.3. Оценка канонических корреляций и канонических величин
12.4. Способ вычислений
12.5. Пример
Литература
Задачи
Глава 13. Распределение некоторых характеристических корней и векторов, не зависящих от параметров
13.1. Введение
13.2. Случай двух матриц Уишарта
13.3. Случай одной невырожденной матрицы Уишарта
13.4. Канонические корреляции
Литература
Задачи
Глава 14. Обзор некоторых других работ по многомерному анализу
14.1. Введение
14.2 Проверка гипотез о ранге и оценка линейных ограничений на коэффициенты регрессии. Канонические корреляции и канонические величины
14.3. Нецентральное распределение Уишарта
14.4. Распределение некоторых характеристических корней и векторов, зависящих от параметров
14.5. Асимптотическое распределение некоторых характеристических корней и векторов
14.6. Главные компоненты
14.7. Факторный анализ
14.8. Стохастические уравнения
14.9. Анализ временных рядов
Литература
Приложение. Теория матриц
1. Определение матриц. Действия над матрицами
2. Характеристические корни и векторы
3. Разбиение векторов и матриц на блоки
4. Некоторые результаты
5. Метод сокращения Дулиттла и метод сгущения по оси для решения систем линейных уравнений
Литература
Предметный указатель